
You Are Probably Using A Sub-Optimal CRC
The designers of serial protocols like USB, Ethernet, CAN, or anything using "CRC-8" or "CRC-16 CCITT" did not have access to information on which CRC polynomials are the best for their bit-size and application, so were chosen on what seemed to be reasonable grounds but are now known to be sub-optimal. It is not necessarily that better polynomials were unknown in academic research but that the information had not reached an industrial design audience.
In fact, it was widely believed that the performance of the polynomials was similar enough that you could just randomly pick one from a list in a book and it would be fine for your application. Koopman said
CRCs have been around for a really long time. You would think that after all these years, the best CRC is a well solved problem. Unfortunately, it isn't really.... Until fairly recently, the compute power wasn't available to do an exhaustive search. ... The other problem is that the literature is poorly accessible to computer engineers, a lot of it is written in dense math that's hard to apply ... So as a result, practitioners mostly use what someone else used and they assume it's good and that turns out to be a bad assumption. And they are unaware of limitations and mistakes in previous work. ... Numerical Recipes in C has table of primitive polynomials that they said these are the ones we know about with no evaluation about whether they are good, bad or indifferent. You can't just pick this stuff from a random list, you actually have to know which ones were good and which were bad. That information was totally unavailable until fairly recently. Several researchers have worked in this area and you had to go to specific publications to find them and they were really hard to access.
Before the computational power was available to exhaustively search for the best polynomials and evaluate them under all message bit pattern combinations, it was considered that as long as the polynomial met a couple of criteria it was likely to be good enough. Those criteria were i) divisibility by (x+1) because it will then detect all odd numbers of bit errors starting with one bit error, and ii) minimize the number of "1" bits in the feedback value because this costs more in terms of XOR gates in the hardware implementation. Both of these criteria have now been shown to adversely affect the choice of polynomial. In other words, if you want the best performance, these are not the most important factors; in many cases the best solution will have neither of these factors.
Whilst divisibility by (x+1) does detect all odd numbers of bit errors, unless you have a reason for requiring that (i.e. evidence that this is a dominant type of error pattern on your network) it trades off performance on even numbers of bit errors to the point that it is not an overall advantage. Specifically, it doubles the undetected error rate for even numbers of bit errors.
Costs of a few XOR gates in hardware or operations in software are not significant compared to the worsening of the CRC performance that you get by choosing a polynomial with a minimum number of "1"s. Wolf and Blakeney showed in 1988 that the properties are improved by many nonzero coefficients.
For example, if you have 4 non zero terms in the polynomial, that means your CRC is guaranteed to be vulnerable to 4-bit errors. If you have 9 non zero terms, it might be able to detect all 7-bit errors.
Before choosing the best polynomial for your specific task, it is worth knowing that there are some performance guarantees:
- Any polynomial with at least two bits set will catch all single bit errors. (HD=2)
- Any polynomial will detect a single burst of errors up to the size of the CRC
- Any polynomial will detect a fraction of longer error bursts of n bits given by (1- 2^-n)
Examples of sub-optimal CRC design
DARC-8 Data Radio Channel, ETSI, October 2002
DARC-8 uses the polynomial 0x9C (in Koopman representation) and has a HD=5 at up to and including 9 bits of data word, with only 34 undetected error patterns at that length. This would be fine if it was used with such short data words, but it is not. DARC-8 data word lengths are 16 to 48 bits, where the HD has fallen to 2 so is only guaranteed to detect all 1-bit errors and some 2-bit errors. In fact, at 16 bit data length, there are 7 undetected 2-bit error patterns and at 48 bits data length there are 66 undetected 2-bit error patterns so this is polynomial is not performing very well.
By instead choosing the polynomial 0x97 (discovered in 1998), the HD can be improved from 2 to 4, for data word lengths 8 bits all the way up to 119 bits, which is the maximum any code can achieve at HD=4. This means that all 3-bit errors are guaranteed to be detected, and some 4-bit errors, which is a big improvement. Koopman showed that weighted probabilities of undetected errors can be improved by a factor of 13 orders of magnitude at the DARC-8 data word lengths and a typical BER of 1e-6.
It might seem difficult to believe that such a huge improvement can come at such a tiny cost (an extra 1 bit, so one extra XOR gate or operation) but Koopman's work has been proven by independent calculation both within his institution and independently from it.

ITU G.704, October 1998
G.704 adopted a CCITT standard polynomial, CCITT-5 0x15 which is optimal up to 10 bits of data word, where it achieves HD=4 but that is its limit, so when used at 3151 bits of data word the HD has fallen to 2 and the number of undetected error patterns is large (330645). This system would be better of adopting the USB 5-bit CRC polynomial 0x12 (July 1997), even though it does not achieve better HD at that length, it is two times better at error detection (159176 undetected).
It is interesting to note that this is despite the CCITT-5 polynomial being divisible by (x+1) which is commonly said to be desirable, and the USB-5 is not. This is because USB-5 is almost twice as effective at detecting 2-bit errors, and although is at a disadvantage for 3-bit errors since CCITT-5 detects all of these, they occur much less often (factor of the BER) so are that much less relevant/weighted.
CRC-8/DVB-S2, ETSI EN 302 307-1, November 2014
CRC-8 Polynomial 0xEA provides HD=4 for data lengths to 85 bits, but after that and up to 119 bit is only provides HD=2 where there are polynomials which go as far as HD=4. Above 119 bits, although it does as well as any other 8-bit CRC in providing HD=2, it has a higher undetected error fraction than others.
Again using the polynomial 0x97 mentioned above, the HD can be improved this time from 2 to 4, for data word lengths 85 bits to 119 bits, which is the maximum any code can achieve at HD=4. This means that all 3-bit errors are guaranteed to be detected, and some 4-bit errors, which is a big improvement. Koopman shows that weighted probabilities of undetected errors can be improved by a factor of 11 orders of magnitude at the 85 to 119 data word lengths and a typical BER of 1e-6.
SMBus, August 2000
Koopman says SMBus also uses CRC-8 Polynomial 0xEA and goes on to say that 0x83 or 0xA6 would be better. But CRC Catalogue has CRC-8/SMBUS listed as poly=0x07 which is Wikipedia Normal form, equivalent to Koopman's 0x83 and links to the specification which clearly states that the polynomial is x^8 + x^2 + x^1 + 1, which is represented by 0x07 in Normal and 0x83 in Koopman form.
Regardless, looking at the suitability of the CRC against the data word length, the messages generally have data words 16 to 40 bits, so it has a good HD of 4 for those cases. But for data packet transfer commands that are 280 bits, the HD drops to 2. Whilst there is no HD=3 or better polynomial for an 8-bit CRC at that length, 0x83 maintains HD=4 to 119 bits, as good as any other, and has a lower number of undetected errors at the 280 bit point - see table below.
Hamming Weight of 1st non zero value
| dataword length (bits) | 0xEA | 0x83 | 0xA6 |
| 16 | 79 (HD=4) | 80 (HD=4) | 1 (HD=3) |
| 40 | 1553 (HD=4) | 1545 (HD=4) | 47 (HD=3) |
| 280 | 306 (HD=2) | 195 (HD=2) | 33 (HD=2) |
We can see that although 0xA6 does not achieve HD=4 at any point, it achieves very low numbers of undetected errors right out to data word lengths of 280 bits. In a particular application, this might be worth trading off for the worse HD, depending on the weighted sum of undetected error probabilities for messages of each length.
XMODEM, 1977
Koopman says XMODEM also uses CRC-8 Polynomial 0xEA but CRC-Catalogue and Wikipedia say that the CRC in XMODEM is 16 bit, with a reference to an earlier 8-bit checksum (not CRC).
The messages have data words 1024 bits long. At that length, no 8-bit CRC will do better than HD=2 but you can at least choose the one with the lowest Hamming Weight, which is polynomial 0x8E or 0xA6 with a weight of 1578, better than 0xEA's weight of 5214, an improvement factor of 3.3x.
If the CRC size could be increased, an 11-bit CRC (0x7DF) will give you HD=3 and a 12-bit CRC (0xB91) will give you HD=4, but to get HD=5 you need at least 22-bit CRC (0x2A952A).
The CRC-16 used by XMODEM is 0x1021 in Normal form, 0x8810 in Koopman form and provides HD=4 out to 32751 data word bits. Whilst you can't improve on HD=4 under those conditions, polynomial 0x8D95 is nearly twice as good in terms of reduced number of undetected errors.
CAN, September 1991
CAN uses a 15-bit CRC, polynomial 0x62CC over a 18 to 82 bit data word (Standard 11-bit ID field frame) or 38 to 102 bits (Extended 29-bit ID frame) which CAN In Automation claims features a Hamming distance of 6 for most messages. They acknowledge that there is a bit stuffing problem that leads to HD=2 for some messages. The CRC is calculated prior to the bit stuffing so although that extends the number of physical bits to 132 (Standard) or 157 (Extended), the logical data word is maximum 102 bits.
The existing CRC polynomial 0x62CC provides the best probability of undetected error at 102 data word bits and HD=6, but the stuffing bits interact with the CRC calculation as Tran has shown. This leads to an undetected error rate of 1.25e-7 when just 2 flipped bits occur. In this case, there is no better 15-bit polynomial that could have been used, and adding an 8-bit CRC in the payload only helps slightly. This is an unusual case in that the most efficient solution to improve the on the provided 15-bit CRC is to add an 8-bit checksum which makes a 2 orders of magnitude improvement in undetected errors, but the best improvement can be made at the cost of using up 2 bytes of payload is a 16-bit CRC. Unfortunately a CRC in the payload doesn't help improve the Hamming Distance.
If you wanted to extend the HD to 7 at 102 data word bits, you would have to go up to a 21-bit CRC.
The problem with the CRC in CAN isn't so much that it is the wrong polynomial but that it has been used wrongly - it should either be applied after bit-stuffing (in which case it is non-optimal, and there is the problem of an unstuffed FCS) or another approach to the bit sync problem should have been used such as per byte start bits.
LonWorks/ANSI/CEA-709.1, 1999
LonWorks uses CRC-16-CCITT, 0x8810 over 64 to 1984 bits data word. This provides HD=4 out to 32751 data word bits but nothing beyond that. The best HD which can be obtained with a 16-bit CRC is HD=16 by 0xEFFF but that is only for 1 data word bit at HD=5 and above, and we can't get to HD=5 for 1984 bits with any 16-bit CRC, the best is 0xAC9A which gets to HD=5 for 241 bits, so again an analysis of data word size by frequency of use is required to decide if this is better.
Chakravarty says that the probability of undetected errors for 64-bit payloads is only about as good as that provided by the optimal 12-bit CRC, and are a factor of more than 7 orders of magnitude worse than an optimal 16-bit CRC.
If we limit ourselves to 64-bit payloads, the best 16-bit CRC would be 0x9EB2 which is HD=6 for up to 135 data word bits, and HW@HD=6 = 9110 compared to 0x8810 HW@HD=4 = 162. To compare these, we have to use the formula
Pud = HW * BER^n * (1-BER)^(c-n)
where Pud is unweighted probability of undetected error, HW is Hamming Weight, BER is bit error rate, n is number of errors, c is bit size of code word. Using BER = 1e-6, I calculate
Pud (0x8810) = 1.6e-22
Pud (0x9EB2) = 9.1e-33
So there is 10 orders of magnitude improvement on the table for free just by choosing a different polynomial. It reduces to a still impressive 8 orders of magnitude if BER = 1e-5.
But we should also look at the maximum payload (1984 bits) and find the best 16-bit CRC for that, which is 0xBAAD because it has goes out to HD=11 for data word 2 bits whilst covering the 64 to 108 bit messages with HD=5, and having a Hamming Weight at HD=4 of 66% of the value of the 0x8810 CRC, which translates to a lower undetected error fraction of this amount.
USB 1.0, 1.1 and 2.0, 1996-2000
USB defines two CRC polynomials; a 5-bit 0x12 Token CRC to cover the token fields, and a 15-bit 0xC002 Data CRC to cover the data field.
The 5-bit CRC covers 11 bits of ADDR and ENDP or frame number in SOF token, but is also used in PING and SPLIT which can be up to 19 bits. Polynomial 0x12 covers 26 bits at HD=3, which is the best HD that can be obtained for this size, and is the optimal choice.
The size of the data field depends on the speed variant in use, low speed is 72 bits, full speed is 520 bits, high speed is 8200 bits.
0xC002 has HD=4 up to 32751 bits so it has more than sufficient coverage, and we can't get coverage of 8200 bits at HD=5. But we could get to HD=6 at 135 bits using 0x9EB2 which would be better than the existing polynomial for the low speed variant. Or by changing to 0xD175 for all variants the Pud could be reduced by a factor of nearly 2 million times, from 5.8e-15 to 3.3e-21 at BER=1e-6. Interestingly, the USB spec has a recommended limit on the BER of 1e-12. Using that BER, the Pud using 0xC002 is 5.8e-39 and using 0xD175 is 3.3e-45
However, in USB the packet ID is sent as a 4 bit ID followed by its bitwise inverse, which allows for a quicker check than performing CRC calculations but only has HD=2. Theoretically that reduces the HD for the whole message to 2, irrespective of the CRCs with HD of 3 and 4 but the USB spec tries to deal with that by requiring no response to unsupported transaction types or directions, making it less likely that a corrupted PID is accepted.
Ethernet IEEE 802.3, 1985
802.3 and many others use "CRC-32", polynomial 0x82608EDB used with MTU of 12112 bits. This gives a Hamming Distance of 4 so all 1,2 and 3-bit errors will be detected. But 223059 4-bit errors out of a possible 9e14 are undetected. But there are five better 32-bit CRCs which all get to HD=6 covering 16360 data word bits. The best one is 0xFA567D89 since it achieves HD=6 at 32736 bits, whilst having the highest length protection (274 bits) at HD=7.
It is difficult to compute the exact improvement in Pud since Koopman does not give Hamming Weight tables for the 0xFA567D89 polynomial past 8192 bits, but in general it should achieve BER^2 lower Pud values. Using our BER = 1e-6 as before, this would be a lower Pud by a factor of 1e-12.
Other notable polynomials for 32-bit CRCs are 0xBA0DC66B which achieves HD=6 to 16360 data word bits and HD=4 to 114663 bits which is more than 9 times the length of an Ethernet MTU; 0xC9D204F5 which achieves HD=4 to 2.1e9 bits; 0xA094AFB5 which protects 19 data bits out to HD=14.
It is also possible to find the smallest CRC that protects 12112 data word bits, and that is 15-bit 0x4306 at HD=4 or 28-bit 0x9037604 at HD=5. In other words, if you are not going use a certain bit-size polynomial to its fullest possible HD, you may as well save some bits which could be used for other purposes. But this does compromise the burst error detection.
Evidence showing sub-optimal polynomial use in non-standard protocols
The previous examples are for standardized protocols where the only people who get to make the design decision are those involved in the standardization committee or who put a good case for their alternative proposal via their national standards institute. Although many protocols in use in industry are standardized, there are very many cases of internal or proprietary protocols being designed and used. Since these are often not publicly available, researchers cannot easily analyse their characteristics.
Koopman did a survey for his FAA report and found companies responses showed that they could often get 1 or 2 bits more HD by choosing a different polynomial of the same size, or could improve the undetected error detection fraction by a reasonable amount eg 1.9x So unless the polynomial was dictated by the need to be compatible with a standard protocol, it is not uncommon to choose a sub-optimal polynomial. Koopman phrases this as "leaving this [improved performance] on the table" since it could easily have been taken up at design time but instead has been squandered because of lack of knowledge.
People are leaving one or two bits of HD on the table. For the exact same computational cost, they could have had one or two bits more of error detection just by changing the CRC polynomial
It might not sound like there is that much difference to be had with 1 or 2 bits of HD, but each bit approximately improves (usually underestimates) the Pud by a factor of the BER, so this is major source of improvement, on top of the burst error performance.
There is a final reason for using (rather than choosing) a sub-optimal polynomial and that is due to a mistake or misprint in the specifying document or implementation. One respondent to the survey mentioned above gave incorrect values for the IEEE 802.3 polynomial, and Koopman also points out that Numerical Recipes in C, 2nd ed gives CRC-12 incorrectly (since corrected). There are known cases of academic papers with incorrect polynomials so the advice is to take a cross reference from multiple sources.
I'll leave you with Koopman's own words
The morals of this story are several fold. Just because someone else is using it doesn’t make it a good idea. Just because it’s a published international standard doesn’t necessarily make it a good idea. Just because it’s optimal for some lengths doesn’t mean it’s what you want to use, you have to look at what’s optimal for your lengths, for your particular situation.
Sources and Analysis
All polynomials above are in Koopman format unless specifically stated otherwise, since they are taken from his tables.
My spreadsheet comparing all known polynomials 3-32 bits at HD=3 to HD=20, compiled from Koopman's data files. Includes table like this, and calculates answers to questions such as What is shortest CRC for this data length?, Find a poly for CRC bitsize x, data length y, etc.
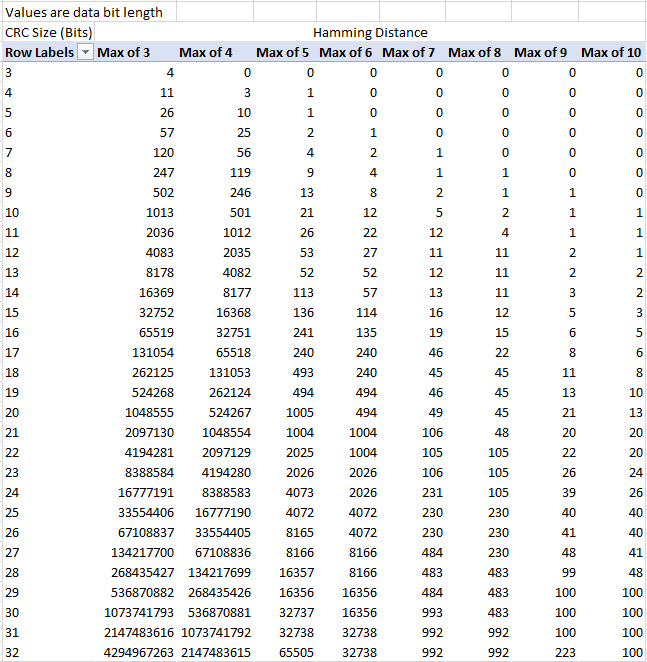
My spreadsheet of Probability of Undetected Errors for all known polynomials 3-16 bits at HD=2 to HD=20, data length to 4096 bits, compiled from Koopman's data files. This includes all the HW data in that range so is large (27 MB) and slow to calculate, you may wish to turn off auto calculate. Allows you to plot your own version of Pud vs data length for chosen polynomials, but these do not have the additional weighting factor that is used by Koopman and Chakravarty since it is unclear how to calculate it, so they don't have their flat plateaus.
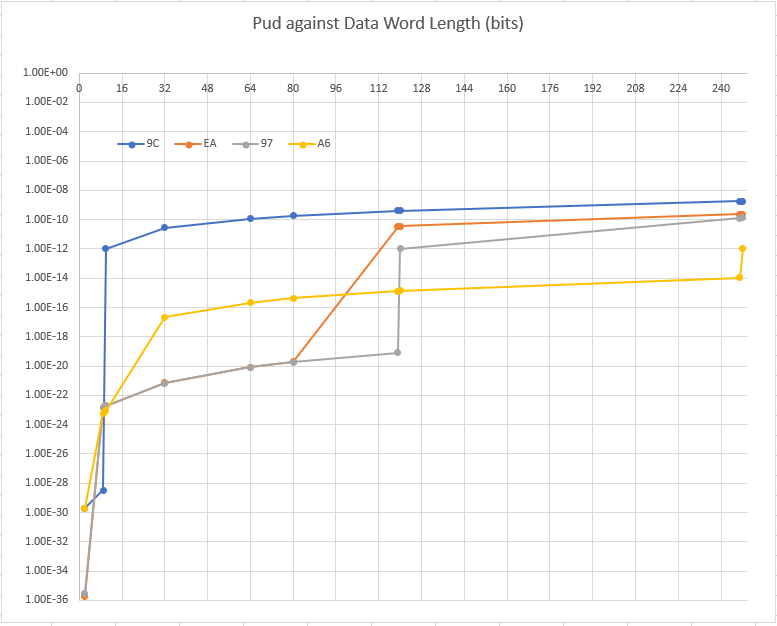
All the source material Data files Copyrighted 2015-2018 by Philip Koopman, Carnegie Mellon University and licenced under Creative Commons Attribution 4.0 International License.