Hitting the Precision Limit of Excel; or 15 Digits Should be Enough for Everyone

Excel is a great all purpose tool, used by maybe 7% of the world's population. From shopping lists to budgets, Gantt charts and calendars to circuit simulators and digital music workstations, it can do it all. It is so good at so many things and so universally available to businesses that in many cases the biggest competition for software startups is not other specialized software solving the same problems but Excel.

When it comes to using Excel for engineering tasks, there are lots of known pitfalls. Treating values as dates, or strings which are supposed to be hex like "51E67" as scientific format is one big category of pitfalls. Another is that although the probability of an error in any one cell is small, when you have a high number of cells all dependent on each other, the probability of error somewhere in the sheet means that the final result is likely to be wrong. The canonical case study is Reinhart and Rogoff, covered by a talk I highly recommend, Emery Berger's "Saving the World from Spreadsheets". So cross checking or auditing become necessary. Use  CTRL-` to switch between formula view and value view.

In common with many computer languages, Excel uses IEEE 754 floating point numbers with 15 digit precision. You would have thought that this would be sufficient for most engineering purposes, where final results are conventionally given to 3 or 4 significant figures. However, it is easy to come a cropper when doing certain calculations. In my case, I hit the 15 digit precision limit when doing probability calculations in the context of detecting errors in a communications channel in the presence of random noise.

Prof Philip Koopman calculates the probability of undetected 4 bit errors per hour in a message with a 16 bit CRC with these formulae

prob_of_n_bit_error = combin(codeword_bit_size,num_bit_errors) * (BER)^num_bit_errors * (1-BER)^(num_good_bits)

undet_errors_per_hour_no_HD_n_coverage = 1-(1-prob_of_n_bit_error)^num_msgs_per_hour

undet_errors_per_hour_with_HD_n_coverage = 1-(1-prob_of_n_bit_error*(HW_of_crc/combin(codeword_bit_size,num_bit_errors)))^num_msgs_per_hour

Typical values are

codeword_bit_size = 528
num_bit_errors = 4
num_msgs_per_hour = 72000
BER = 1e-8
num_good_bits = 524
HW_of_crc = 64510

with results

prob_of_n_bit_error = 3.2e-23
undet_errors_per_hour_no_HD_n_coverage = 2.3e-18
undet_errors_per_hour_with_HD_n_coverage = 4.6e-23

and the problem is that Excel will calculate the last two variables as zero. It comes unstuck at (1-3.2e-23)^7200 which gets evaluated as 1 because of the loss of precision, where it should be 0.9999999999999999997696000000000000000265383935999999999...

The solution is to use a plug-in which gives you a much higher precision such as xlPrecision which has versions for 25, 1500 or 5000 significant digits, or even more if you want.

Once you've installed xlPrecision, you can convert the formula =(1-3.2e-23)^7200 to =xlpPOWER(xlpSUBTRACT(1, 3.2E-23),7200) to get the result 0.9999999999999999997696000000000000000265383935999999999... and go on to use the xlp functions to correctly evaluate the probabilities. I can say correctly because the figures in this sheet then agree with Prof Koopman in the video at this point.

These values are very small. It might be thought that these are as close to zero as makes no practical difference, but that is not true because they have a real-world impact. Prof. Koopman works in field of safety critical systems such as aviation and self driving cars, and in these areas we have to keep the probability of possibly fatal accidents down to very low numbers across all deployed systems and for many operating years. These two factors multiply up the number of incidents so we need to start from a low base rate. He says the catastrophic failure probability limit given in FAA AC 25.1309 is 1e-9 per flight hour. This might seem low but compare it with 10,000 systems operating for 20 years continuously which is 1.75e9 item⋅hours.

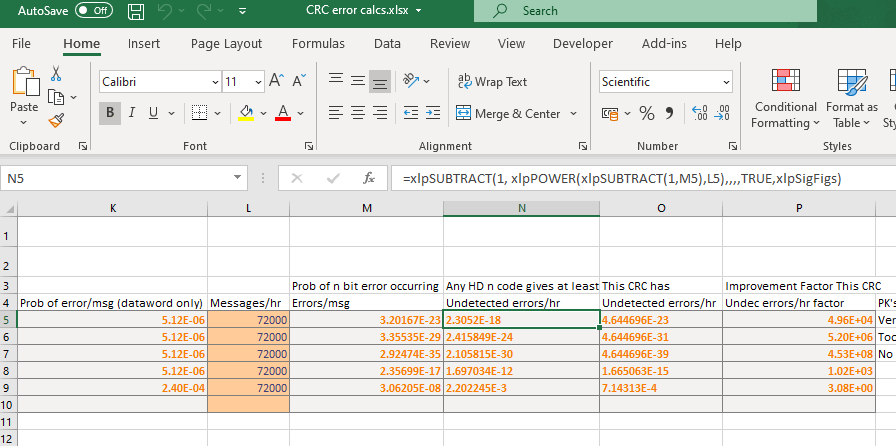
Some examples of using CRCs to improve the undetected errors by a factor of ~50,000 or more are given in this spreadsheet on the ProbOfError page. Columns N and O are where the xlPrecision functions are required to avoid Excel's 15 digit precision completely destroying the results, and allows for a final improvement factor to be calculated. Bear in mind that Column G, undetected errors is from Koopman's Hamming Weight files and has to be looked up manually, in this version of the spreadsheet.

As Prof. Koopman says himself on page 45 of his report to the FAA

Note that these computations require care with regard to numerical accuracy. Spreadsheet arithmetic often gives inaccurate answers with large exponents. A more accurate numerical tool should be used when evaluating these probabilities.

xlPrecision gives you that increased precision, without you having to abandon the use of spreadsheets.